A fizika az a tudomány, amelyik minden lehetségest meg akar mérni. Ha pedig megmérte, akkor ugye ezt dokumentálni is kell. Ennek legegyszerűbb formája olyan táblázat kitöltése, amely a szépen elrendezve tartalmazza a mért adatokat.
Vegyük elő a legegyszerűbb mozgás úgynevezett út-idő és sebesség-idő táblázatait és grafikonjait.
Először az út-idő grafikont, más szóval a megtett út függését az időtől és a sebesség függését az időtől, megint más szóval az utat és a sebességet az idő függvényében. Figyeljetek, ez ugyanaz, csak más megfogalmazásban! Nem kell semmit klülön megérteni, nem kell semmit külön megmagyaráznom, ez csak szóhasználat, árnyalatnyi különbség!!!
Pl: Állandó sebességű mozgás út-idő összefüggése
| 1. mérés | 2. mérés | ... | n. mérés | |
| út (km) | ||||
| idő (óra) |
Látjátok, az 1. mérés alá kell beírni a mért km adatot és az alatta levő cellába az idő adatot.
1/ Nagyon FONTOS, hogy a mért mennyiség mellé a mértékegységet is beírjátok, mert így lesz egyértelmű az, hogy mit is mértél. Nem mindegy ugye, hogy a beírt 12 az métert vagy mérföldet jelent. Ha pl. méterben is van mérési eredmény, akkor azt számold át pl. km-re. Vagy éppen a km-t méterre. Legyen mindig azonos mértékegységben a táblázat adata. Ugyanígy az idő mellé is írd be, hogy órában mérsz, vagy éppen másodpercben (mint itt).
Általában tehát a fizikai mennyiség mellé minden esetben kötelező beírni a mértékegységét is.
2/ a 4. oszlopban ... -ot láttok. Ez mindig azt jelenti, hogy oda bármennyi darabszámú oszlop is kerülhet. 2, 7, 22, vagy éppen 47. ... tehát tetszőlegesen sok. A végén pedig az n. mérés ezekben az esetekben 5, 10, 25, 50. Ezzel az n-nel jelölitek, hogy mennyit akartok mérni. Itt első + második + 2 mérés, tehát az n pontosan 5 lesz.. Itt első + második + 7 mérés, tehát az n pontosan 10 lesz. Itt első + második + 22 mérés, tehát az n pontosan 25 lesz. Végül az első + második + 47 mérés, tehát az n pontosan 50 lesz. Ezzel azt meséltem el, hogy n értéke TETSZŐLEGESEN NAGY lehet.
3/ Természetesen egy címet is meg kell adni, ami a címtől elvárhatóan informálja az olvasót, mit is kell ott figyelnie.
4/ Szinte mindig az időmérés kezdetekor kezdődik az út mérése. Tehát a 0 sec időhöz 0 m megtett út tartozik.
Ezek után töltsük ki a táblázatot (egyenes vonalú egyenletes mozgás esetére)
Állandó sebességű mozgás út-idő összefüggése
| 1. mérés | 2. mérés | 3. mérés | 4. mérés | |
| út (m) | 50 | 100 | 900 | 5000 |
| idő (sec) | 1 | 2 | 4,5 | 10 |
Látod, hogy szépen, logikus sorrendben, érthetően szerepelnek a mérések. Bárki ránéz a táblázatra, láthatja, értheti, miről szóltak a méréseid. Minden egyértelmű, azonnal tudsz sebességet (út/idő) számolni, átlagokat számolni, sorba rendezni.
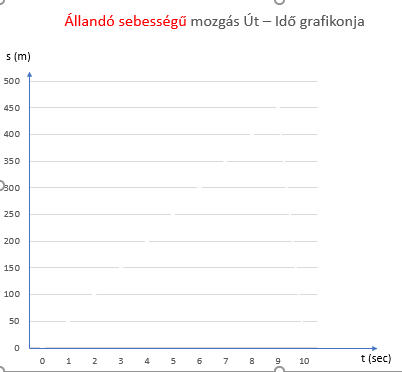
Ezek után jöjjön a grafikus ábrázolás, hiszen sokan a rajzokat jobban szeretik, mint a táblázatokat és tényleg, sokszor több információt rövidebb idő alatt le lehet olvasni egy rajzról, grafikonról.
Itt is vannak kötelezően betartandó szabályok.
- a mérési eredményeket egy függőleges és egy vizszintes tengelyt tartalmazó ábrába kell berajzolni. Az összetartozó értékek fognak egy pontot jelenteni. Az előbbi táblázatból az 1 h és az 50 km tartozna az első berajzolandó ponthoz.
- meg kell mondani, mit ábrázolsz a tengelyeken, a kis nyíl környékére oda kell írni a fizikai mennyiséget, vagy annak a jelét. Esetünkben az idő, a t a mérés egyik tárgya. A másik tengelyen a mért megtett utat méred, tehát az út jelét az s-et írod oda.
- meg kell adni ezek mértékegységét. Itt a t-t sec-ban, az s-et m-ben mérjük. Ezt kell zárójelben a tengelyre, a fizikai mennyiség mellé odaírni. Tehát s (m) és t (sec).
- be kell skálázni, tehát meg kell adni, egy rovátka mennyi egységet jelent. Itt ezen a grafikonon ez magától értetődik.
- szinte kivétel nélkül 0-val kell kezdeni a két tengely metszéspontjánál.
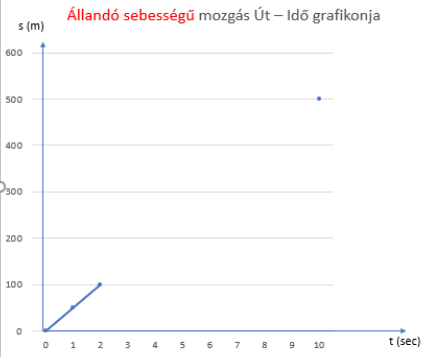
Most kezdjük el berajzolni a pontokat, az összetartozó értékek szerint.
A tengelyek metszéspontjánál a 0;0 amint mérés nélkül is nyilvánvaló.aA
Az időtengelyen 1-et megyek jobbra és 50-et felfelé, mert 1 másodpercnél 50 m-t mértem. Utána megint 1 sec-ot megyek jobbra és 50 km-t felfelé, mert 2 másodpercnél 100 méter a mérési eredmény.
És így tovább a többi pontnál.

Tehát 10 sec-nál 500 m. Látod, hová teszem az utolsó pontot, 10 sec érték felett az 500 m-nél kell berajzolnom.
Ahogy a mozgás elnevezéséből következtethető, a grafikonja is egyenletes => egyenes.
Éppen ezért ez az egyenes arányosság. Megint azt írom, hogy más szóval két változó között akkor van egyenes arányosság, ha a hányadosuk állandó. Az út és idő hányadosa állandó. Ez a jellemző állandő érték a mi mostani esetünkben a sebesség.
Ennek megfelelően ha a sebesség állandó, akkor a táblázat:
Állandó sebességű mozgás sebesség-idő összefüggése
| 1. mérés | 2. mérés | 3. mérés | 4. mérés | |
| út (m) | 50 | 100 | 900 | 5000 |
| idő (sec) | 1 | 2 | 4,5 | 10 |
| sebesség (m/sec) | 50 | 50 | 50 | 50 |
és a grafikon: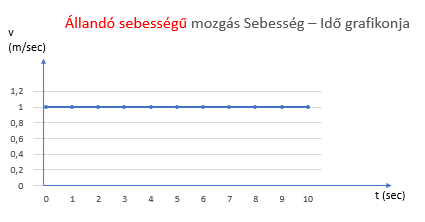
No most hagyom abba, gondolom, elfáradtatok. Másodszorra már könnyen meg fogjátok érteni és az itt tanult fogalmak, jelölések, ábrázolások később a matematikában is, a fizikában is használhatók lesznek. Sőt, még a társadalomtudományokban is olvashattok sok ilyet, amelyet akkor majd játszi könnyedséggel tudtok értelmezni.
RÁADÁS - nézzétek meg, ti is meg tudjátok magyarázni az okát:
1/ Az út-idő grafikon meredeksége annál nagyobb, minél nagyobb a sebesség. Általánosságban is; minél nagyobb az egyenes arányosság (= a hányados) értéke, annál meredekebb az ezt ábrázoló egyenes.
2/ a sebesség az egyenes vonalú egyenletes mozgásnál a grafikonon egy vizszintes egyenes. Minél nagyobb a sebesség (= a hányados) értéke, annál magasabbra kell rajzolni ezt a vizszintes egyenest.