Erről a témáról muszáj rendszerezettebben írnom, mint a tankönyv. A környezetünkben annyi gép van, és ezek között annyi nem is tűnik annak, ami pedig az életeteket könnyíti meg. Ezek helyes, jó helyen történő alkalmazása, sok időt, energiát takarít meg nektek.
Egyszerű gépek
Definíció: Az egyszerű gépek oyan eszközök, melyekkel kedvezőbbé tehetjük az erőhatás nagyságát, irányát, támadáspontjának helyét.
Az energiamegmaradás általános érvényű törvény, tehát minden egyszerű gépre is igaz. Annak a ZÁRT rendszernek is állandó az energiája, amelyben valamelyik egyszerű gépet alkalmazzátok. Tehát nincs energiaváltozás, nincs különbség az egyszerű géppel és az anélkül végzett munka mennyiségei között! Ez más szóval azt jelenti, hogy az egyszerű géppel munkát nem lehet megtakarítani!!! CSAK erőt, amint a fenti meghatározás is mondja.
A munka az erő és az elmozdulás szorzata. Ha fele annyi erőt fejtünk ki (a teherre) az egyszerű géppel, akkor kétszer annyi úton mozgatjuk a tárgyat/terhet. Ezt sok gépen megfigyelhetitek.
Az egyszerű gépek fajtái:
Megkülönböztetünk emelő és lejtő típusú egyszerű gépeket.
EMELŐ – a tengely körül elforgatható rúd
- Egykarú emelő – pl. talicska, diótörő, sörnyitó, emberi alsókar
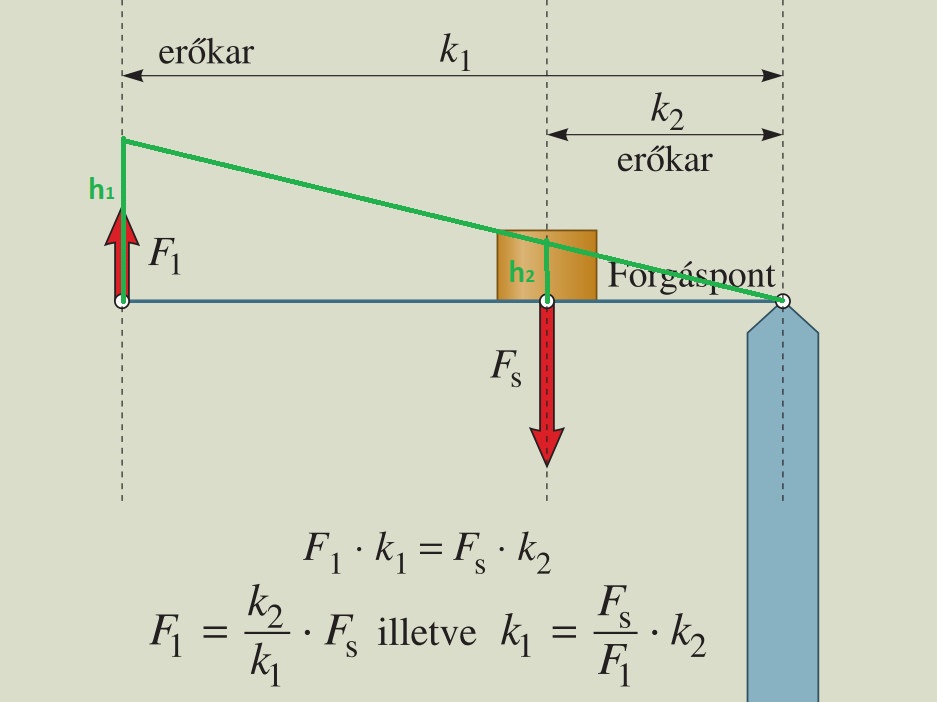
- Kétkarú emelő – pl. gémeskút, mérleghinta, olló, mérleg Ismétlés: FORGATÓNYOMATÉK
- Hengerkerék – pl. kerekeskút (henger és a végén kerék közös tengellyel)
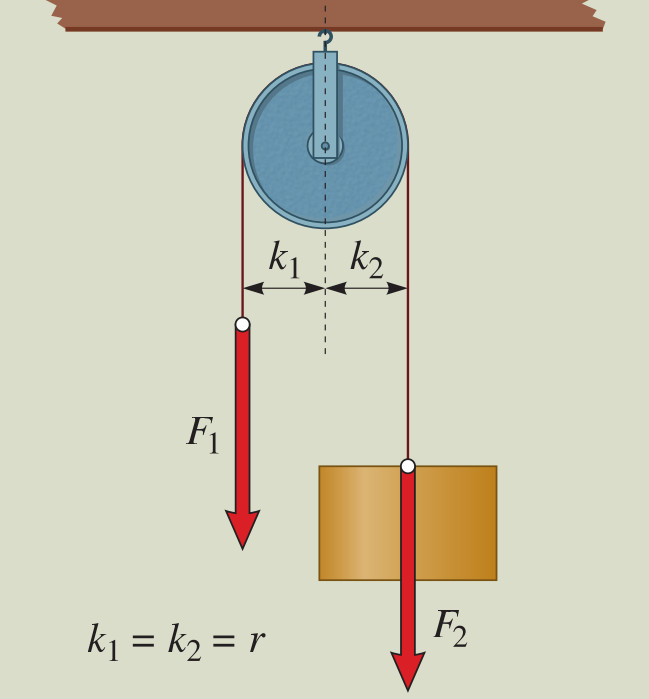
- Csiga – pl. lift, malteros vödör – csigasor
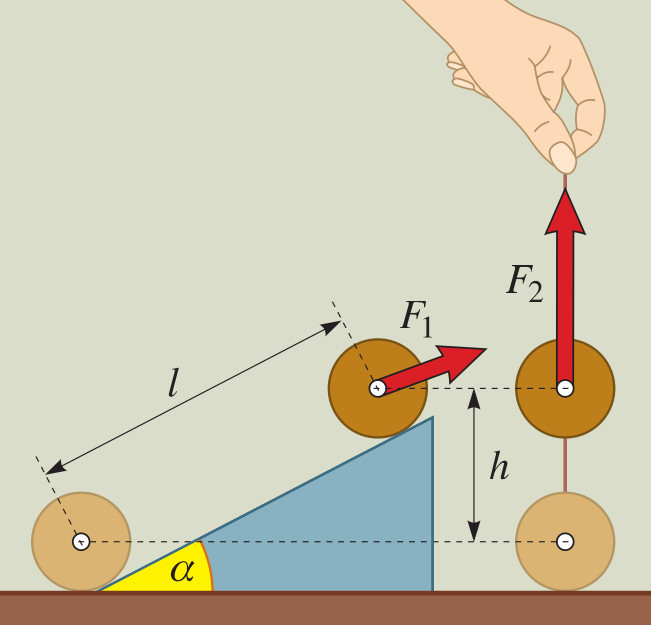
LEJTŐ – a vízszintessel hegyesszöget bezáró sík felület
- Ék – pl. véső, balta, sőt kés és tű
- Csavar – hengerre felcsavart lejtő
Forgatónyomaték
 |
Gondoljunk a hintára, a kanyarodó biciklire, az emelőrúdra. Órán is találkoztunk már hasonlóval, a karos-mérleggel. Mi ebben a hasonló? Nos a testet erővel, erőhatással nem csak húzni/tolni lehet, hanem forgatni is. Ha az erő hatásvonala nem megy át a test adott forgástengelyén és nem is párhuzamos vele, akkor ennek az erőnek forgató hatása van, ez az erő elfordítja a testet. Mint a libikókánál. A kormány forgatása elfordítja a biciklit, az emelő lenyomása felemeli a másik végén levő terhet. |
A forgató hatás annál nagyobb,
- minél nagyobb erővel történik és
- minél messzebb van a támadáspont a tengelytől.
Ezt az egyszerű forgatási mértéket forgatónyomatéknak hívjuk és M-mel jelöljük. Az előbbi megfigyelés következtében az M=F*k képlettel számoljuk. F: a forgató erő, k: az erő hatásvonalának távolsága a tengelytől. Ezt a k-t erőkarnak is hívják. Mértékegysége: Newtonméter, Nm.
Az előbbit egy definícióban is összefoglalhatjuk: Forgatónyomatéknak nevezzük az erő és erőkar szorzatát. Tehát az erő forgató hatását. !!! k>0
Ha a hintát nézzük, akkor gyerekkorunkból emlékezhetünk, hogy a nagyobb súlyú hintázót csak akkor lehetett felemelni, ha őt közelebb ültettük a tengelyhez. Az egyik erőkart éppen teherkarnak is lehet hívni. Ekkor már mondhatjuk is a gyakorlati alkalmazást, Fe * ke = Ft * kt. Itt e az erőre, t a teherre utal. Az egyenlőség fejezi ki az egyensúlyt. Tehát ha a két előbbi szorzat egyenlő, akkor a karosmérleg vagy a hinta vízszintes/egyensúlyi helyzetben van.

Ennek nagy jelentősége van az egyszerű gépeknél. Fele akkor erővel megtudjuk emelni a terhet emelőrúddal, ha az alátámasztási ponttól kétszer akkora távolságra nyomjuk le azt.
Forgatónyomaték = erő * erőkar. (M=F*k) Akkor van egy mérleg egyensúlyban, ha a két oldalán az erők/súlyok és erőkarok szorzata egyenlő. Így az adott terhet/súlyt fele akkora súllyal tudom kiegyensúlyozni, ha a teherkarhoz (kt) viszonyítva az fele akkora súlyhoz tartozó teherkar (ke) kétszer akkora. F*ke = 2F * kt/2
Tehát emelőre alkalmazva ezt a mondatot: az adott terhet/súlyt fele akkora emelőerővel tudom felemelni, ha a teherkarhoz (kt) viszonyítva az én erőkarom (ke) kétszer akkora. F*ke = 2F * kt/2
Az emelő típusú egyszerű gépnél az egyik az erőkar, a másik a teherkar.
Számolós példák
|
Egykarú emelő:
|
Mekkora munkával tudom felemelni az 50 kg tömegű fémtömböt az ábra szerint, ha a tömb 50 cm-re van a forgástengelytől, míg én az 1,5 m hosszú rúd végén emelem? Tehát az 50 kg tömböt 16,6 kg tömegnek megfelelő erővel tudom felemelni pl. 30 cm magasra. Ha a tömbnél emelném, akkor W2 = F2 h2 = Tehát igazoltam, hogy munkát nem tudok megtakarítani, hiszen a harmadannyi tömeget háromszor nagyobb úton mozgatom. Ehhez a hasonló háromszögek alapján tudtam a h1 és h2 értékek arányát kiszámolni. |
|
Állócsiga:
|
Mekkora munkával tudom felemelni az 50 kg tömegű fémtömböt az ábra szerint, ha a tömb 5 cm-re van a forgástengelytől (10 cm sugarú a csiga)? F1 * k1 = F2 * k2, ahonnan F1 = F2 * k2 / k1 = 500 N A munka pedig szintén ugyanaz, mert a rajzból is látszik, hogy annyival emelkedik a fémtömb, amennyivel a kötelet húzom. Tehát az F * s szorzat értéke nem változik.
|
|
Lejtő:
|
Igazoljátok, hogy azonos munkát végeztek az ábra szerinti két esetben, ha a lejtő tetejére felemelitek, illetve felvonszoljátok az 50 kg tömegű fémtömböt. A felvonszoláshoz 250 N erő szükséges. A lejtő 50 cm magas és az α szög 30°. (az ábrán látható, hogy F1 vektor feleakkora, mint F2 vektor) EMELÉS: F2 = 500 N => W2 = F2 * h = 500 N * 0,5 m = 250 Nm. VONSZOLÁS: Ha α = 30°, akkor ez olyan egyenlő oldalú háromszög oldala, amelyben ’h’ az oldal fele. Ha nem tanultátok, rajzoljátok le ezt a (derékszögű) lejtőt, tükrözzétek a talajra és mérjétek le az ’l’-t és a ’h’-t is. Mindkét esetben ugyanazt az eredményt számoltam ki. 250 Nm, akár emelem, akár felhúzom a lejtő tetejére. Ez elég nyilvánvalóan mutatja, hogy a lejtő egyszerű gép sem takarít meg munkát. Feleakkora az erő, de kétszer akkora az elmozdulás ebben a szituációban! |
|
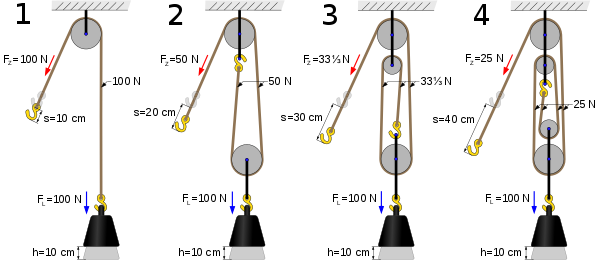
Csigasor:
|
Egy mozgócsiga terhelése a két kötélág között egyenletesen oszlik meg, tehát egy kötélre a terhelés fele jut. Az n mozgócsigából álló csigasor utolsó állócsigájáról lefutó kötél meghúzásához a teher n-ed részének megfelelő erőre van szükség. Itt a Wikipedia.org-ból kimásolt rajzon most n = 1,2,3,4. FZ a teher emeléséhez szükséges erő, Ha a teher emelkedése h, a kezelő kötél végét s hosszú úton kell meghúzni. A kettő közötti összefüggés: s = n * h. (10, 20,30 és 40 cm) Csigasorral sem tudunk munkát spórolni, mert amennyivel kisebb erővel emeljük a terhet, annnyival hosszabb úton húzzuk a kötelet. A csigasorral végzett munka a sima emeléssel végzett munkával egyenlő n értékétől függetlenül, amint a behelyettesítés mutatja: |
Örökmozgó = perpetuum mobile
Ez már nem tananyag. Annak ajánlom a figyelmébe, akit érdekel egy kicsit a tudomány.
Mindenütt kiszámoltuk, hogy a kiszámolt munkamennyiség ugyanaz ezeknél a mozgásoknál az eszközök alkalmazásával is és anélkül is. Tehát igazoltuk amit az elején állítottunk, hogy ezeknél
az egyszerű gépeknél is igaz az energiamegmaradás törvénye.
Ha pedig igaz, akkor örökmozgót nem lehet készíteni. Ezt jól jegyezzétek meg! Ennek bizonyítása most még nehéz számotokra, de évszázados tapasztalat és az energiamegmaradás általános érvénye miatt ezt el kell fogadnotok. A súrlódás, a légellenállás létezése a legyszerűbb indok, ami azt jelenti, hogy a gépek mozgása során bizonyos, bármennyire is kicsi energia erre fordítódik, tehát a gép működése egy idő után leáll. A hatásfok nem lehet 100 %, nagyobb pláne nem lehet, a gépekből nem lehet több energiát, munkát kinyerni, mint amit beletettünk.
A középkor, az újkor talán az egyik legnagyobb célkitűzése az aranycsinálás után az örökmozgó, ismert latin nevén a perpetuum mobile megalkotása volt. Ezt ha egyszer megindítják, akkor külső ráhatás, hajtóanyag betáplálása nélkül mozgásban marad, és lehetőség szerint költségmentesen hajtóteljesítményt is szolgáltat az emberiségnek. Gondoljátok el, milyen büszkeséget jelentene a feltalálójának - és persze óriási hasznot is hoz neki.
Amíg be nem bizonyítják, hogy ez nem lehetséges, addig nem lehet tudni, hogy egy adott út tévút-e. Ez sok-sok próbálkozás után csak később lesz bizonyosság, később oszlik el a kétely. Azt a tanulságot kell levonnotok ebből , hogy a tévút megtétele, az útkeresés sem tökéletesen haszontalan, hiábavaló. Ezen a tévúton is sok hasznosat, értelmeset lehet találni. Ezért nem szabad a kísérletezést, az új megismerését feladni, abbahagyni. Mi haszna van egy (utólag bebizonyosodott/bizonyított) tévedést kutatni, megismerni, tanulmányozni?
- kezdetekben egyáltalán nem tudni, tévút lesz-e,
- a tévedésből tanulni/okulni lehet, (az okos más kárán tanul, a buta a sajátján)
- más felfedezés is kijöhet belőle,
- ötleteket adhat bárkinek,
- természetesen használható részeredmények is létrejöhetnek.
Általában is, ha valami nem sikerül nektek, akkor utána nem az elkeseredés a következő teendő, hanem az elemzés.
- Mi volt, amit rosszul csináltam és miért?
- Milyen külső okok játszottak szerepet a 'kudarc'-ban?
- Mit tudok én javítani, hogy a következő sikeres legyen?
- ...
- Ha a fentiekre nincs jó válasz, hogy tudom elkerülni az ilyen eseteket?
és hasonló kérdések.
Feladni nem szabad! A rosszat elkerülni, javítani kell, a jót pedig megőrizni, megtanulni, gyakorolni kell!
Hf: Munkafüzet 31. oldal 1., 32. oldal 2. és 33. oldal 6. feladatok