Olvassátok el ezt a posztot, amely két nagyon hasznos tudnivalót is tartalmaz.
Meg kell válaszolni az itt a címben feltett kérdést, a kézenállás nyomásának kiszámolása után.

Azért küldöm ezt a bejegyzést, mert a fizikai gondolat, megközelítés kifejtésére jó alkalom nyílik a válaszadás közben. Ezt a két gondolatot a végén fogod majd olvasni - remélem, eljutsz odáig, nem fogy el a türelmed!

Az első lépés kijelenteni, hogy két kézen és két lábon fogok számolni.

Azután következik annak számbavétele, hogy mi szükséges a válaszadáshoz. Nos a nyomás kiszámításához meg kell mérnünk a 1/ nyomóerőt és a 2/ nyomott felületet, mert a képlet szerint
p = F_ny/A.

1/ Az F_ny nyomóerő természetesen a súlyomból származik. Lemérem, vagy tudom, hogy én 90 kg vagyok az otthoni mérlegen. Ebből következően 900 N (newton) erőt fejtek ki a talajra, hiszen megtanultuk, sokszor alkalmaztuk: 1 kg tömeg 10 N súlyerőt képvisel.          Vigyázat: 1 kg = 10 N nagyon nem korrekt egyenlőség!!!!!

2/ a nyomott felület a kezemet jelenti, mert pontosan ilyen nagyságú felületen nyomom a talajt, tehát pontosan ekkora nagyságú a nyomott felület. Ezt a fura alakú felületet nehéz megmérni. Tehát közelítést alkalmazok: helyettesítem a kezemet egy téglalappal. Körbe rajzolom, a bennfoglaló téglalapot rárajzolom és lemérem ennek oldalait. Ez nálam 8 cm és 22 cm. Még a hüvelykujjamat is körbe rajzolom. Ez egy 1,5 cm széles és 7 cm hosszú téglalapot adott. Ily módon a kezem felülete (8cm * 22cm) + (1,5cm * 7cm)= 186,5 cm2. A nyomás mértékegységében m2 szerepel, tehát ezt átváltom m2 -re. Megszorzom még 2-vel, hiszen két kézen fogok állni. A = 0,0373 m2.

Kézenállásnál a nyomás tehát 900N / 0,0373m² = 24,13 Pa.

A talpon állás esetére a cipőmnél is megmérhetem a felületet, de a kérdés csak az, hogy hasonlítsam össze a két esetet, nem pedig adjam meg mindkét értéket. A mérést meg tudom spórolni, ha alkalmazom a megtanult ismeretet, mely szerint ugyanazon nyomóerő esetén annál nagyobb a nyomás, minél kisebb a nyomott felület. Ránézésre is nagyobb a cipőm felülete, mint a kezemé, tehát 'kézenfekvő' a válasz,
vagyis az utolsó lépés: a lábon állás esetén kisebb a talajra kifejtett nyomásom! Ezzel fejeztem be a házi feladatot.

Ha mégsem tudod a dőlt betűvel írt összefüggést, akkor számolnod kell. Ugyanazt teszed a cipőddel. Ennek eredménye pl. 9 cm * 31 cm => a két cipőddel 0,0558 m²-n nyomod a talajt. Ebben  az esetben A = 0,0558 m². Lábonállásnál a nyomás 900N / 0,0558m² = 16,13 Pa. Tehát így is ki tudtad hozni az előbbi eredményt: a lábon állás esetén kisebb a talajra kifejtett nyomásod! 

Itt következik a két fizikai gondolat/elv:

1/ Azt látjuk, hogy a pontos mérés helyett közelítést alkalmaztam. Ezt sokszor meg lehet tenni, hiszen nem az egzakt érték érdekel bennünket! Általánosan igaz, hogy a mérés, a választott mérőeszköz pontosságát, a kísérlet kivitelezésének tökéletességét  az adott helyzet, szükséglet, követelmény határozza meg.
Ha össze kell szorozni 12-t és 5-öt, akkor azt fejben megoldjuk, nem vesszük elő a kalkulátort, pláne nem a számítógépet egy Excel táblával. Ha az a kérdés, hogy milyen hosszú az íróasztalod, mert kérdés, hogy befér-e a szekrény mellé, akkor mielőtt elkezdenéd tologatni, a lehető leggondosabban leméred egy vonalzóval, vagy szabócentivel - milliméter pontossággal. A milliméter pontosság kell ide. De ha a haverod kérdi ugyanezt, csak úgy kíváncsiságból, akkor elég lesz az araszoddal méricskélni. Hiszen elég annyit válaszolni, hogy kb. 115 cm.

2/ A kéz hasonlít a téglalaphoz, tehát a hasonló, de nekünk megfelelőbb, könnyebben kezelhető szituációt hoztam létre. Ezt hívják a természettudományokban MODELLEZÉSnek. Egy a probléma szempontjából kielégítően hasonló, de sokkal könnyebben kezelhető környezetet hoztam létre és itt adtam választ az engem érdeklő problémára. Itt következik a természettudományokban elfogadott logikai lépés: Ha a modellben igaz az állításom, akkor az eredeti szituációban is ugyanúgy igaz. Most ne menjünk tovább, ne boncolgassuk, mi van ha valaki ezt megcáfolja. Arról később beszélünk majd, például a fénytannál.

A modellt persze tényleg alapos megfontolás után lehet csak kiválasztani, mert világos, hogy a rossz modell téves állításokat eredményez. Erre szoktam én mondani, hogy az emberre melyik a jobb modell? A szabóbábú vagy az oroszlán?
Ha méretekről, arányokról, statikáról van szó, akkor a bábú. Ha életfolyamatokról, biológiáról van szó, akkor pedig az oroszlán.
Ebből mindenképpen jegyezzétek meg azt, hogy az adott természettudományi kérdés határozza meg a használható modellt.

Az sem baj, ha nem tudsz kézen állni, hiszen ezt a helyzetet igen könnyű elképzelni ahhoz, hogy megtedd a szükségeset és megadd a választ.

Alább látjátok, mit tart mindenképpen megjegyzendőnek a tankönyv, milyen alapvető dolgokat kell mindenképpen tudnod a későbbiekben az erőkről.

Energia

4-ről 5-re javítás is energia, a sportolás is energia, az evés is energia. Mind változást hoz létre a környezetben. Ez a változtató képesség az energia. Az idők során kiderült, hogy az életünk legfontosabb fogalma az energia. Ezért fontos vele alaposan foglalkozni.

Az energia = változtató képesség             jele E     mértékegysége: joule, J, kJ, 1000 J = 1kJ        0,3 kJ = 300 J.

A reggeli kávém mozgási, helyzeti, belső energiáját is tudom változtatni! Kirohanok vele a konyhából, számhoz emelem, melegítem. Rugalmas vagy mező energiája nincs ☹.

A mezők energiáját leginkább a kölcsönhatásaikon láthatjuk/mérhetjük. Pl. az elektromos és mágneses vonzás/taszítás mozgást eredményez. A gravitáció pedig függőlegesen gyorsítja a tárgyakat.

Energiák egymásba alakíthatók – leggyakoribb a mozgási => belső energia átalakulás

Energiamegmaradás

Az energia megmaradás törvénye – az egyik legfontosabb fizikai elv!

Energia nem keletkezik és semmisül meg, csak az egyik energiafajta a másik fajtává alakul.

Erről napokig, hetekig lehet beszélni, most azonban csak ennyivel kezdjünk, lényeg, hogy ismerkedjetek a fogalommal, szokjátok az energiával kapcsolatos gondolatokat. Amennyire lehet, nézzétek át alaposan a fenti ábrát, ez segít az energiával ismerkedésben.

Az energia kapcsán nem lehet megkerülni az ilyenfajta kérdéseket: zöld energia? megújúló energia? kimerül a Föld energiatartaléka?

Az ember ökológiai lábnyoma

Az a földterület, amelyre évente az embernek szüksége van, hogy a szükségleteit megtermelje, előállítsa.

Országonként, földrészenként más és más. Ez a mostanság kitalált fogalom azt méri, hogy mennyi természeti energiát használunk a mindennapjainkban. Amint sejtitek, ez egyre nő. 1960-ban egy földlakóra vetítve ez az érték 0,8 hektár volt, ami 2014-re 2,2 hektárra nőtt.

A Föld elméleti eltartóképessége (létszám/földterület) személyenként 2014-ben 1,8 hektár volt. Tehát becslések szerint túlléptük a Föld eltartóképességét. Mit lehet akkor csinálni? Hogyhogy mi mégis békében itt élünk és mi bizony nem vesszük észre ezt a 'kinövést'? Aki erről ír egy házi dolgozatot, ötöst kap tőlem.

Túllövés napja: Az a nap az adott évben, amikor elérjük/felhasználjuk/kimerítjük a számunkra a Föld által biztosított energia mennyiséget. 2014-ben augusztus 20. volt.

• Legyen életünk része az energiatakarékosság, energiatudatosság. Helytelen és káros válasz, hogy én egyedül mit érek a tudatosságommal. Erre igaz maradéktalanul a mondás: Sok kicsi sokra megy!!!

Apró kiegészítés: a teljes folyamatot, ciklust kell mindig nézni a környezetvédelemben, az energiatudatos viselkedésnél. Pl. a ma divatos elektromos autó ugyan a fosszilis energiával (kőolaj) spórol, a károsanyag kibocsátást, ezáltal a légyszennyezést csökkenti. Ennek fejében ez az autó több elektromos áramot használ fel és ennek az elektromos áramnak az előállítása, szállítása az erőművekben növeli a környezetszennyezést. Tehát az igazi megoldás nem az elektromos autó, hanem a bicikli, a tömegközlekedés, az autókölcsönzés!

Bizonyára olvassátok, halljátok, hogy az emberiség (és főleg a 15-30 éves korosztály) egyre nagyobb része környezetvédő, másik része pedig tagadja ennek fontosságát. A környezetvédők azt mondják - egyre hangosabban -, hogy a klímakatasztrófa elkerülhetetlen, a másik tábor pedig kamunak, svindlinek, a világ elitje összeesküvésének állítja be a jelenséget. Kinek higgyél?

A téma nagyon összetett, emellett sokféle nézőpont, értékelési szempont létezik. Ezért lehet olyan sokféle véleményt felhozni.
Én személy szerint a környezetvédők mellett állok, saját magam is környezettudatosan élek. Látom, hogy a zöldek sok túlzó érvet használnak. Határozottan azon a véleményen vagyok, hogy a Föld állandóan változik, most éppen egy melegedési folyamatban élünk, DE sajnos az emberi tevékenység ezt a nélkülünk is létező folyamatot sajnos nagyon-nagyon felgyorsította. Sok jel mutatja számomra, hogy tényleg az utolsó pillanatokban lehetünk, amikor még tehetnénk valamit. Ha pedig az egyén a maga egyéni szintjén nem tesz meg mindent az említett folyamat ellen, akkor "magunk alatt vágjuk a fát".

Nézzétek meg ezt a két sokkoló videót:

Katt ide<<<, vagy probléma esetére: https://www.youtube.com/watch?v=jYOhXH5vouI

A második mutatja, hogy nem is kell olyan messze menni a szemétszigetet megnézni:
Katt ide<<<, vagy probléma esetére: https://www.youtube.com/watch?v=0S-r1jVv0ik

Ha van kedved, időd, energiád, oldd meg ezeket a feladatokat a szünet magányában! Leosztályozom és ha tetszik a jegy, be is írom a naplóba. Ezzel javíthatsz.

1. Írd le a tehetetlenség törvényét!

…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

2. A vízvezeték-szerelő a régi ólomcsövet ugyanakkora méretű műanyag csőre cseréli Hasonlítsd össze ólom- és a műanyag cső tömegét és sűrűségét! A válaszadáshoz alkalmazd a relációs jeleket (< > = ) a ? mellett.

                        Az ólomcső tömege m_ó     ?     a műanyag cső tömege m_m

                        Az ólomcső ϱ_ó                  ?     a műanyag cső sűrűsége ϱ_m

3. A Hold anyagából vett minta tömege 82,5 g, térfogata 25 cm³. Mekkora a sűrűsége?

4. Az 1 m hosszú acélrúd tömege 61,7 kg. Az acél sűrűsége 7,8 g/cm³ . Mekkora az acélrúd térfogata?

5. Miben nyilvánul meg az alábbi esetekben a test mozgásállapotának a megváltozása? Írd a megfelelő választ a mondatok után:
   a. A futball-labda visszapattan a kapufáról …………………………………………………………………………..
   
   b. Az autóversenyző elindul az egyenes pályán …………………………………………………………………….
   
   

6. Írd be a mennyiségek nevét, jelét, mértékegységét a táblázatba a megfelelő üres helyre!

7. Az asztalon egy dinnye van. Ábrázold a három rajzon egy-egy nyíllal

a dinnye súlyát; a tartóerőt; a dinnyére ható gravitációs erőt!

8. A kezünkben tartott, nyugalomban lévő kő 3 N erővel nyomja a kezünket. Mit állapíthatunk meg a kezünk által kifejtett ellenerő irányáról és nagyságáról?

• Iránya: ............................................................................................................................
• nagysága: .......................................................................................................................

 9. Milyen tényezőktől függ a súrlódási erő nagysága?

• ........................................................................................................................................
• ........................................................................................................................................

 10. Az esőcsepp először gyorsuló mozgással, majd egy bizonyos idő után egyenletes mozgással közeledik a föld felé. Mi az a hatás, amely miatt az esőcsepp sebessége nem nő tovább?

........................................................................................................................................................

 11. Állapítsd meg, melyik esetben van, melyik esetben nincs fizikai értelemben vett munkavégzés! Válaszaidat írd a mondatok után!

• Korcsolyázunk. ................................................................................................................
• Leckét tanulunk. ..............................................................................................................
• Felmegyünk fel a dombra. .................................................................................................

12. A traktor 40.000 kJ munkát végez, miközben 1,6 km utat tesz meg szántás közben. Mekkora erőt fejt ki a traktor?

Erről a témáról muszáj rendszerezettebben írnom, mint a tankönyv. A környezetünkben annyi gép van, és ezek között annyi nem is tűnik annak, ami pedig az életeteket könnyíti meg. Ezek helyes, jó helyen történő alkalmazása, sok időt, energiát takarít meg nektek.

Egyszerű gépek

Definíció: Az egyszerű gépek oyan eszközök, melyekkel kedvezőbbé tehetjük az erőhatás nagyságát, irányát, támadáspontjának helyét.

Az energiamegmaradás általános érvényű törvény, tehát minden egyszerű gépre is igaz. Annak a ZÁRT rendszernek is állandó az energiája, amelyben valamelyik egyszerű gépet alkalmazzátok. Tehát nincs energiaváltozás, nincs különbség az egyszerű géppel és az anélkül végzett munka mennyiségei között! Ez más szóval azt jelenti, hogy az egyszerű géppel munkát nem lehet megtakarítani!!! CSAK erőt, amint a fenti meghatározás is mondja.
A munka az erő és az elmozdulás szorzata. Ha fele annyi erőt fejtünk ki (a teherre) az egyszerű géppel, akkor kétszer annyi úton mozgatjuk a tárgyat/terhet. Ezt sok gépen megfigyelhetitek.

Az egyszerű gépek fajtái:

Megkülönböztetünk emelő és lejtő típusú egyszerű gépeket.

EMELŐ – a tengely körül elforgatható rúd

• Egykarú emelő – pl. talicska, diótörő, sörnyitó, emberi alsókar
• Kétkarú emelő – pl. gémeskút, mérleghinta, olló, mérleg Ismétlés: FORGATÓNYOMATÉK
• Hengerkerék – pl. kerekeskút (henger és a végén kerék közös tengellyel)
• Csiga – pl. lift, malteros vödör – csigasor

LEJTŐ – a vízszintessel hegyesszöget bezáró sík felület

• Ék – pl. véső, balta, sőt kés és tű
• Csavar – hengerre felcsavart lejtő

 Forgatónyomaték

Gondoljunk a hintára, a kanyarodó biciklire, az emelőrúdra. Órán is találkoztunk már hasonlóval, a karos-mérleggel. Mi ebben a hasonló? Nos a testet erővel, erőhatással nem csak húzni/tolni lehet, hanem forgatni is. Ha az erő hatásvonala nem megy át a test adott forgástengelyén és nem is párhuzamos vele, akkor ennek az erőnek forgató hatása van, ez az erő elfordítja a testet. Mint a libikókánál. A kormány forgatása elfordítja a biciklit, az emelő lenyomása felemeli a másik végén levő terhet.

A forgató hatás annál nagyobb,

• minél nagyobb erővel történik és
• minél messzebb van a támadáspont a tengelytől.

Ezt az egyszerű forgatási mértéket forgatónyomatéknak hívjuk és M-mel jelöljük. Az előbbi megfigyelés következtében az M=F*k képlettel számoljuk.      F: a forgató erő, k: az erő hatásvonalának távolsága a tengelytől. Ezt a k-t erőkarnak is hívják. Mértékegysége: Newtonméter, Nm.

Az előbbit egy definícióban is összefoglalhatjuk: Forgatónyomatéknak nevezzük az erő és erőkar szorzatát. Tehát az erő forgató hatását. !!! k>0

Ha a hintát nézzük, akkor gyerekkorunkból emlékezhetünk, hogy a nagyobb súlyú hintázót csak akkor lehetett felemelni, ha őt közelebb ültettük a tengelyhez. Az egyik erőkart éppen teherkarnak is lehet hívni. Ekkor már mondhatjuk is a gyakorlati alkalmazást, F_e * k_e = F_t * k_t. Itt e az erőre, t a teherre utal. Az egyenlőség fejezi ki az egyensúlyt. Tehát ha a két előbbi szorzat egyenlő, akkor a karosmérleg vagy a hinta vízszintes/egyensúlyi helyzetben van.

Ennek nagy jelentősége van az egyszerű gépeknél. Fele akkor erővel megtudjuk emelni a terhet emelőrúddal, ha az alátámasztási ponttól kétszer akkora távolságra nyomjuk le azt.

Forgatónyomaték = erő * erőkar. (M=F*k) Akkor van egy mérleg egyensúlyban, ha a két oldalán az erők/súlyok és erőkarok szorzata egyenlő. Így az adott terhet/súlyt fele akkora súllyal tudom kiegyensúlyozni, ha a teherkarhoz (k_t) viszonyítva az fele akkora súlyhoz tartozó teherkar (k_e) kétszer akkora. F*k_e = 2F * k_t/2

Tehát emelőre alkalmazva ezt a mondatot: az adott terhet/súlyt fele akkora emelőerővel tudom felemelni, ha a teherkarhoz (k_t) viszonyítva az én erőkarom (k_e) kétszer akkora. F*k_e = 2F * k_t/2
Az emelő típusú egyszerű gépnél az egyik az erőkar, a másik a teherkar.

Számolós példák

Örökmozgó = perpetuum mobile

Ez már nem tananyag. Annak ajánlom a figyelmébe, akit érdekel egy kicsit a tudomány.

Mindenütt kiszámoltuk, hogy a kiszámolt munkamennyiség ugyanaz ezeknél a mozgásoknál az eszközök alkalmazásával is és anélkül is. Tehát igazoltuk amit az elején állítottunk, hogy ezeknél
az egyszerű gépeknél is igaz az energiamegmaradás törvénye.

Ha pedig igaz, akkor örökmozgót nem lehet készíteni. Ezt jól jegyezzétek meg! Ennek bizonyítása most még nehéz számotokra, de évszázados tapasztalat és az energiamegmaradás általános érvénye miatt ezt el kell fogadnotok. A súrlódás, a légellenállás létezése a legyszerűbb indok, ami azt jelenti, hogy a gépek mozgása során bizonyos, bármennyire is kicsi energia erre fordítódik, tehát a gép működése egy idő után leáll. A hatásfok nem lehet 100 %, nagyobb pláne nem lehet, a gépekből nem lehet több energiát, munkát kinyerni, mint amit beletettünk.

A középkor, az újkor talán az egyik legnagyobb célkitűzése az aranycsinálás után az örökmozgó, ismert latin nevén a perpetuum mobile megalkotása volt. Ezt ha egyszer megindítják, akkor külső ráhatás, hajtóanyag betáplálása nélkül mozgásban marad, és lehetőség szerint költségmentesen hajtóteljesítményt is szolgáltat az emberiségnek. Gondoljátok el, milyen büszkeséget jelentene a feltalálójának - és persze óriási hasznot is hoz neki.

Amíg be nem bizonyítják, hogy ez nem lehetséges, addig nem lehet tudni, hogy egy adott út tévút-e. Ez sok-sok próbálkozás után csak később lesz bizonyosság, később oszlik el a kétely. Azt a tanulságot kell levonnotok ebből , hogy a tévút megtétele, az útkeresés sem tökéletesen haszontalan, hiábavaló. Ezen a tévúton is sok hasznosat, értelmeset lehet találni. Ezért nem szabad a kísérletezést, az új megismerését feladni, abbahagyni. Mi haszna van egy (utólag bebizonyosodott/bizonyított) tévedést kutatni, megismerni, tanulmányozni?
- kezdetekben egyáltalán nem tudni, tévút lesz-e,
- a tévedésből tanulni/okulni lehet, (az okos más kárán tanul, a buta a sajátján)
- más felfedezés is kijöhet belőle,
- ötleteket adhat bárkinek,
- természetesen használható részeredmények is létrejöhetnek.

Általában is, ha valami nem sikerül nektek, akkor utána nem az elkeseredés a következő teendő, hanem az elemzés.
- Mi volt, amit rosszul csináltam és miért?
- Milyen külső okok játszottak szerepet a 'kudarc'-ban?
- Mit tudok én javítani, hogy a következő sikeres legyen?
- ...
- Ha a fentiekre nincs jó válasz, hogy tudom elkerülni az ilyen eseteket?
és hasonló kérdések.

Feladni nem szabad! A rosszat elkerülni, javítani kell, a jót pedig megőrizni, megtanulni, gyakorolni kell!

Munka

1/ Szellemi munka, fizikai munka, munkavégzés, hasznos munka, otthoni munka, nyári munka, feketemunka. Mind valamilyen energiát, erőkifejtést jelent. Bennünket most a fizikai munka érdekel, amit mérni is szeretnénk.
A fizikai munkánál van erő is ÉS elmozdulás is. Tehát hiába akarom eltolni a páncélszekrényt, ha nem mozdul, nincs munkavégzés.

2/ Az energiaváltozás is munkát jelent. Munka következtében jön létre az energiaváltozás. Ez lehet
-- állapotváltozás – pl. hőátadás és
-- mechanikai munkavégzés – elmozdulással jár.
-- rengeteg más energiaváltozás is létezik, de azokat most nem tárgyaljuk.
Más megfogalmazásban: Munkavégzés következtében bekövetkező energiaváltozást munkának nevezzük. Ez a fizikai munka fogalmat írja le, sok helyen olvasható, de ez alapján még nem tudom mérni a  munkát. Márpedig a fizikában ugye 'mindent' mérni akarunk. Ezért a következő meghatározást használjuk, ezt jegyezd meg!

DEFINÍCIÓ: Fizikai értelemben akkor végzünk munkát, ha az erő hatására az erő irányában elmozdulás jön létre.
Ez szerepel a tankönyvben. Én inkább úgy fogalmazok, hogy mechanika munkát akkor végzünk, ha az erő hatására az erő irányában elmozdulás jön létre. A teljesítménynél (4-5 bekezdéssel lejjebb) fogok egy érthető példát mesélni (%%-kal jelölöm), akkor látni fogod, miért kell értened mindkét formulát. 

A munkát W betűvel jelöljük a fizikában. Tehát a fenti két szempont érvényesülését (1/ erő, 2/ erő irányú elmozdulás) vizsgáljuk, vagyis az elmozdulással járó munkavégzést. Ez mindig erőhatás következtében jön létre. Formálisan:  F =>  elmozdulás/sebességváltozás/gyorsulás
Mérések és példáink, tapasztalatok alapján leírhatjuk:

W ~ F és W ~ s             => W = F * s                  !!! s itt az elmozdulás és nem az út!!! Ráadásul az erő irányába eső elmozdulást kell számolni! (~ az arányosság jele)

Innen látszik, hogy mértékegysége a Nm. Ezt elkeresztelték: ez a joule, J.      1000 J = 1kJ,  300 J = 0,3 kJ, 1000 kJ = 1 MJ = 1 Megajoule. Kiejtése: zsúl, dzsúl.

Vigyázat, harmadszor írom: itt F és s egyirányú, Tehát az erő irányában történő elmozdulás számít csak. (kiskocsi, szán)

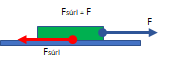
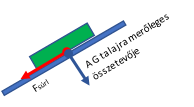
Fh a számunkra alkalmas irányú húzóerő, Fv pedig ennek a talajjal és az elmozdulással párhuzamos összetevője. A kiskocsi húzása közben Fv * s munkát végzünk a munka most tanult definíciója szerint.

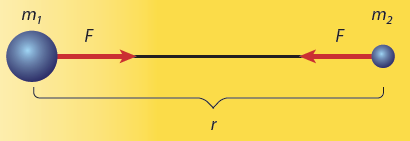
Pótlás, ismétlés: Newton második törvénye szerint F = m* a, A testre kifejtett erő egyenlő a test tömegének és az erő által létrehozott gyorsulásnak a szorzatával.

Az emelési, gyorsítási munkát vizsgáljuk részletesebben egy-egy kis példa segítségével, mert fontos megértenetek, mi az, amikor az erő és az elmodulás egy irányba esnek/mutatnak.

Emelési munka: 3 kg tömegű táskát 2 m magas polcra emelek. Mennyi a munkavégzés? Mennyi az energiaváltozás?
m = 3 kg (tehát a gravitációs erő ellenében kifejtett erőm 30 N.)
h = 2 m
-----------------
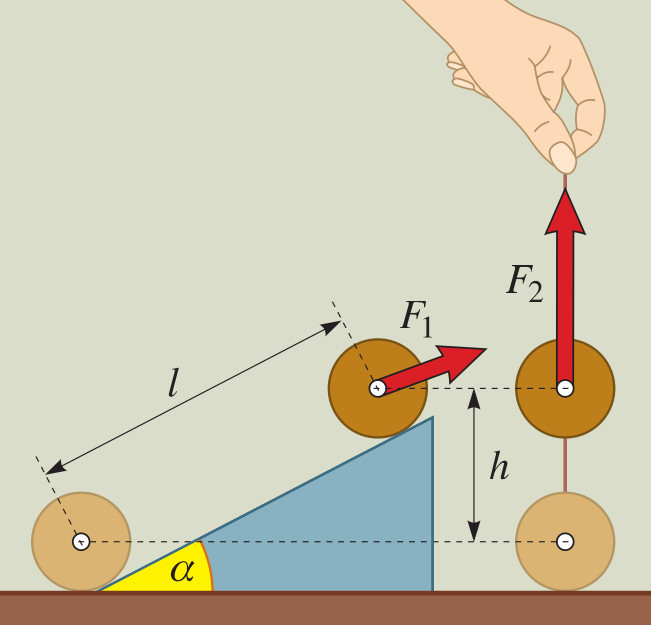
W = ?            W = F * s = m* g * h                              itt F = m*g és h - a magasság - az elmozdulás, mert a gravitációs erő ellenében végzem a munkát. A gravitáció függőleges és függőlegesen emelem a táskát, tehát az erő és az elmozdulás egy irányba mutat.
W = 3 kg * 10 m/sec² * 2 m = 60 m²kg/sec² = 60 Nm = 60 J             (mkg/sec² helyére behelyettesítheted a N-t)
Ez azt is jelenti, hogy a táska (helyzeti) energiája 60 J-lal nőtt meg.

Gyorsítási munka: 2500 kg tömegű autót 54 km/h sebességre egyenletesen gyorsít a motor. Mennyi munkát végez eközben?
m = 2500 kg
v = 54 km/h = v_v                                      
v_átl = (0 km/h + 54 km/h) / 2 = v_v / 2 mivel egyenletesen gyorsul fel 0-ról 54 km/h sebességre.

W = F * s = (m * a) * s = m * (v_v / t) * v_átl * t = m * v_v * v_átl = m * v_v * v_v / 2 = ½ m * v_v² =
2500 kg / 2 * (54 km / h)² = 1250 kg * 225 m²/sec² = 281250 Nm = 281,25 kJ. Ennyi munkát végzett a motor és ennek következtében a kocsi mozgási energiája is ennyivel nőtt.

Következtetés 1: Mekkora erővel lehet 900 J munkát végezni 15 m úton?
W = 900 J
s = 15 m
----------------------------
F = ?            Alkalmazva a már megtanult képletet (W=F*s), átosztva   F = W / s. = 900 Nm / 15 m = 60 N.
60 N erővel lehet 15 m úton 900 J munkát végezni.

Teljesítmény, hatásfok

Megállapodtunk az előbb, hogy fizikai munkát akkor végzünk, ha a testre erővel hatunk, amely azt elmozdítja. Ebből következően a fizikában a mechanikai (fizikai) munkát az erő (F) és az erő hatására történt, az erővel megegyező irányú elmozdulást (s) összeszorozzuk.

A munkával kapcsolatban lényeges fogalom a teljesítmény és a hatásfok. Erről beszéljünk most. A köznapi beszédben azt mondjuk, hogy minél gyorsabban végezzük a munkánkat, annál nagyobb a teljesítményünk. Minél több elültetett gyümölcsfánk hoz termést, annál nagyobb a tavaszi előkészítésünk hatásfoka. A fizikában is ezeket az értelmezéseket fedi az egzakt definíció. A teljesítmény fontos mutató, mert ez alapján könnyebb, objektívebb összehasonlítani a gépek hasznosságát, vagy akár az emberek erejét, munkabíró képességét. Ugye inkább használod azt a gépet/autót, amelyik az 500 kg terhet 2 perc alatt vontatja el 10 km távolságra, mint amelyik 15 perc alatt.  

DEFINÍCIÓ: A teljesítmény a végzett munka és a munkavégzéshez szükséges idő hányadosa.
A fizikában ugye mindent mérni akarunk, tehát a teljesítményt is kiszámoljuk az előbbi meghatározás segítségével. Ez a mondat pedig a köznapi fogalomnak tökéletesen megfelelő P = W / t képletet eredményezi.  

A teljesítmény jele a P (power), mértékegysége a J/sec, amit wattnak kereszteltek el (W=watt).
Az erőművek teljesítménye MW (megawatt).  1 MW = 1.000 kW = 1.000.000 W.

Sajnos a munka jele is W, vigyázzatok, ne keverjétek a kettőt.

%% Az izzó 60 wattos, az azt jelenti, hogy ez az izzó másodpercenként 60 Joule elektromos energiát alakít át fény- és hőenergiává. A mai lecke szóhasználatával: a világítás közben másodpercenként 60 J munkát végez.
1 W = 1 J / 1 sec. Hogy tud egy lámpakörte munkát végezni? Hol van itt az erő és az elmozdulás? Jó kérdés. Ezt később fogjuk megtanulni, nincs semmi baj, tévedés. Egyelőre azt vedd figyelembe, amit az előbb a fizikai értelemben vett munkánál írtam.

Hatásfok

DEFINÍCIÓ: A hatásfok a hasznos munkának és a befektetett munkának a hányadosa. Tulajdonképpen a munkavégzés eredményessége. Viszonyszám.
Mivel viszonyszám, nincs mértékegysége! Jele: η (éta)

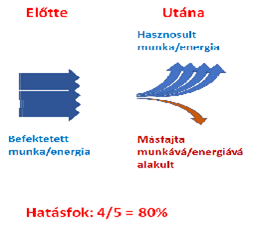
Szemléletesen: Át kell vinned egy pohárban 10 l vizet egyik vödörből a másikba. Nyilván kilötykölöd a vizet, miközben a két vödör között közlekedsz. Tehát amikor már kiürítetted a 10 literes első vödröt, akkor a földön tócsa is van. A második vödörben csak pl. 9,6 liter gyűlik össze. Ebben az esetben hasznos munkának csak a 9,6 l-hez szükséges munkát lehet tekinteni, míg a  befektetett munka a 10 'liternyi' munka volt. 9,6/10=0,96.
A hatásfok 0,96. Ezt százalékban is kifejezheted: 96%.

Tudjátok, hogy a régi lámpakörte forró, amikor világít. Valószínűleg hallottad azt is, hogy a régi típusú izzók világítási hatásfokánál sokkal jobb hatásfokú a LED izzó. Képzeld el, a régi hatásfoka 3-5 % volt! Tehát a 60 wattos lámpakörtének csak a 3-5 %-a, vagyis 1,8-3 W fordítódik a fény kibocsátásra, a többi hőtermelésre fordítódik. A befektetett energia/munka 60 J, a hasznos munka/energia 3 J.
Ha a melegítést tekintenénk a lámpa hasznos eredményének, akkor a hasznos munka 57 J, a befektetett munka pedig változatlanul a 60 J.

A hatásfok a definíciója miatt nem lehet nagyobb 100 %-nál!

De nem lehet nagyobb 100 %-nál az ENERGIAMEGMARADÁS miatt sem.

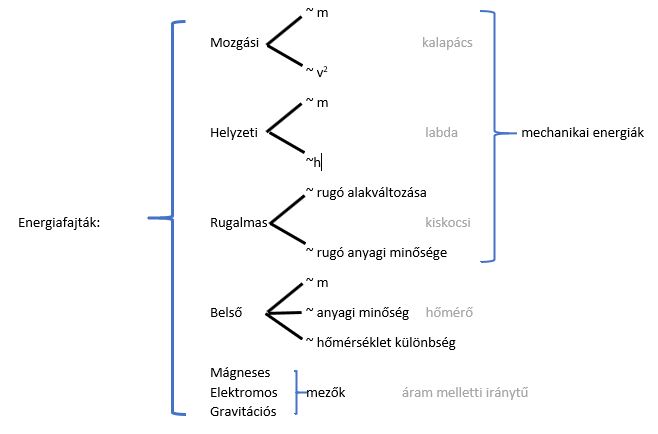
Mechanikai energia

Az energia és az energia megmaradás általános természettudományi elv annyira fontos, hogy ezt külön posztban írom le nektek.

Szorgalmi:

Egyszerű példák:
1 m-ről leejtett labda 60 cm magasra pattant. Akkor a labda helyzeti energiája 60 %-ban hasznosult.

A 2 kg tömegű vödörrel felhúzunk 10 l vizet (10 kg). A befektetett munkánk a 12 kg felhúzása. A hasznos munkánk pedig a 10 kg víz. Teát ezzel a vödörrel 10kg/12kg = 83,3 %. 10 dkg tömegű műanyag vödörrel ugyanez a hatásfok 99% (10kg/10,1kg)

Ha ezt az 5 vödröt 1 óra alatt pakolom meg a homokkal, akkor 5-ször nagyobb a teljesítményem, mintha 5 óra alatt tettem volna meg ezt.
Ha a homok vödörbe lapátolásához W = 50 kJ munka kell, akkor 5 órán keresztül 50 kJ/5 óra = 10 kJ óránként,
1 órán keresztül 50 kJ/1 óra = 50 kJ óránként a teljesítményem.
Tehát a rövidebb idő nagyobb teljesítményt eredményez.

A közelünkben rengeteg teljesítményt látunk. 60 W-os a régi lámpaizzó, 5 W-os a LED izzó. 1200 W-os a hajszárító és 85 kW egyátlagos autó teljesítménye (ezt a forgalmiban ki tudod keresni).

Ha a 60 W teljesítményű izzó 8 órán át világít, akkor mennyi a végzett munka?
A 60 W az áramfelvétel, ez alakul át fény- és hőenergiává.
P = 60 W
t = 8 óra = 28.800 sec
_______________________
W = ?                                                      Ismerjük a definícióból a P = W / t képletet. Ebből W = P * t
W = 60 W * 28.800 sec = 1.728.000 W sec = 1.728.000 J = 1.728 kJ      (W sec = J / sec * sec)
Ezt kényelmesebb mértékegységben is felírhatom: 60 W * 8 óra = 480 Wh (wattóra)

Az erő definíciója úgy szólt, hogy az a testeknek olyan egymásra hatása, amely alak, vagy mozgásállapot-változásban nyilvánulhat meg.
        Emlékezz, mit jelent a feltételes mód: kis erővel ráütsz az asztalra, nem történik semmi. Ugye nem felejtetted el, ez is erőhatás. Hiszen kezed nehézségi erejével hatottál az asztalra. Csak éppen kis erővel.

ISMÉTLÉS: Az alakváltozást, nem kell magyarázni. A mozgásállapot-változás pedig azt jelenti, hogy a test sebessége vagy helyzete változik. Azt is megbeszéltük, hogy ha állandó erővel húzol (hatsz) egy testet, akkor az gyorsulni fog. Épp ez az erőmérés egyik módja. A tömeg és a gyorsulás alapján tudod pl. mérni az erőt. Ez Newton II. törvénye, F = m * a.

Tehát az erő gyorsítja a testet, vagyis növeli a mozgásállapotát (mert sebessége fokozódik). Ilyen erő lehet a gépkocsinál a benzinmotor hajtóereje, vagy a szabadesésnél a gravitáció ereje, a Föld vonzóereje. Azonban a gépkocsinál is, a szabadon eső ejtőernyősnél is fellépnek ezt a mozgást akadályozó erők. Ma ezekről írok nektek. Gépkocsi megáll, ha nem nyomják tovább a gázpedált. Az ejtőernyős pedig egy maximális sebességnél mégsem gyorsul tovább. biztos láttatok ilyen filmet, amikor az ejtőernyős "vigyázzállásban" gyorsan zuhan és amikor kezét-lábát szétterpeszti, lassabban esik. Ezekről fogunk a fizikai törvényszerűségeket felhasználva gondolkozni.

Súrlódás és közegellenállás

Nézzük meg akkor, mi is ez a két fogalom.

DEFINÍCIÓ: A csúszási súrlódás is és a légellenállás/közegellenállás is az egymáson elmozduló és egymással érintkező testek között nyilvánul meg, csökkenti az egymáshoz viszonyított sebességüket.

A csúszási súrlódás szilárd testek között, a közegellenállás gázok/folyadékok és szilárd testek között jön létre.

A csúszási súrlódás értéke mérhető. Ehhez az adott testet a vele érintkező felületen egy erőmérővel egyenletes sebességgel kell vontatni.

A csúszási súrlódás akkor érvényesül, áll fenn, ha a testet már mozgatjuk. De amíg nem sikerül mozgatni, amíg meg nem tudjuk mozdítani, addig a tapadási súrlódás érvényesül.

A tapadási súrlódás egyenlő nagyságú és ellentétes irányú azzal az erővel, amellyel az adott tárgyat meg akarjuk mozdítani.

Ezt kihagyhatod, mert ezt majd középiskolában fogod így, részletesen tanulni és ha ezt nem tudod, ettől még lehetsz kiváló szakács.
Váratlan lehet, de kövessük a folyamatot például egy szekrénynél. Kis erővel tolod, meg sem mozdul. Persze, mert a tapadási súrlódás akadályozza. Növeled a tolóerőt. Még mindig nem mozdul - ugyanazért. Még jobban nekiveselkedsz, végre elindul. A tapadási súrlódási erő tehát igazándiból egy maximum. Annak az erőnek a maximuma, ami még nem tudja megmozdítani a testet - most a szekrényt. Gondold el, azért a maximum érték,
- mert ha nem így definiálnánk, akkor határozatlan lenne az értéke. Ez pedig a fizikában nagyon nem elfogadott!
- mert így pontosan mérni lehet.

A tapadási súrlódás miatt tudunk járni. Lépés közben a lábunk (cipőtalp) hátra nyomja a földet. Az pedig a hatás-ellenhatás törvénye (Newton III.) szerint lábunkat előre nyomja.

A súrlódás nem mindig a mozgást akadályozó erő. Pl. Teherautó platóján a láda pont a súrlódás miatt nem csúszkál össze-vissza. A vitorlást viszi/sodorja előre a szél a légellenállásnak köszönhetően.

Ez IS FONTOS! A súrlódási erő mindig párhuzamos az érintkező felületekkel, a nyomóerő pedig mindig merőleges a felületre, tehát az ábrán látható módon kell berajzolni. Kiszámítását később tanuljuk meg.

A piramisok építése során a hatalmas kőtömbök alá gerendákat tettek. Az egyiptomiak már tudták, hogy a gördülési súrlódás kisebb, mint a csúszásnál fellépő súrlódási erő. Tehát meg kell különböztetnünk a kettőt.
Ennek leglátványosabb megnyilvánulása a gépkocsikerék! Ez a hatásos fékezés technikájának alapja és ezen a tényen alapul az ABS (Anti-Blocking System) működése.

A másik mozgást akadályozó erőhatás a közegellenállási erő. Ez a közegellenállási erő amellyel a folyadékok, gázok fejtenek ki a bennük mozgó testekre. 

A közegellenállási erővel jellemezzük a közegellenállást, ami függ:

• a közeg sűrűségétől
• a testnek a közeghez viszonyított sebességétől
• a testnek a haladásra merőleges keresztmetszetétől
• a test alakjától (lásd áramvonalasság - az ejtőernyős alakjánál is ezt látjuk).

1] kenőanyagok ezt csökkentik, mert az egyenetlenségbe 'behatolva' a felületet símává teszik.

Gyorsítás

Térjünk vissza az erő sebességváltoztató hatására. (A sebesség vektor, tehát az erő a sebesség nagyságát is és irányát is megváltoztathatja.)  A már tanult Newton II. törvénye szerint az erő és az általa létrehozott gyorsulás egyenesen arányos. A hétköznapi életben ezt igazolod is, hiszen minél nagyobb gyorsaságot, gyorsulást akarsz elérni, annál nagyobb erővel lököd meg például a hintát.

A könyvben nem szerepel, tehát ezt sem kell tudnod, de megemlítem. Azért érdemes lenne tudnod: A tapadási, a csúszási és a gördülési súrlódási erő függ az anyagi minőségtől. Ezek egzaktul, pontosan nem mérhető tulajdonságok. Ilyen esetben használja a fizika a tényező fogalmát. Jelen esetben a tapadási, a csúszási és a gördülési súrlódási tényezőt. Használják még az együttható elnevezést is a tényező helyett. Ez mindig egy viszonyszám, vagyis nincs mértékegysége. Még százalékban is ki szokták fejezni. Hányad része? = hány százaléka? A munkafüzet 30. oldalán egy táblázatban van is egy-két ilyen adat. Azt mondja meg
- a tapadási súrlódási tényező, hogy a tapadási súrlódási erő hányadrésze a nyomóerőnek,
- a csúszási súrlódási tényező, hogy csúszási súrlódási erő hányadrésze a nyomóerőnek,
- a gördülési súrlódási tényező, hogy gördülési súrlódási erő hányadrésze a nyomóerőnek.
A közegellenállás függ a test alakjától, a keresztmetszettől, a sűrűségtől. E miatt ez nagyon bonyolult összefüggés. Itt már nem lehet egyetlen közegellenállási tényezőt megadni, definiálni.

Az előző posztban ígértem egy érdekességet. Nos kettő is lesz belőle és itt mindjárt leírom.
1/ Az előző lecke elején azt írja a könyv, hogy az erőhatás testek olyan egymásra kifejtett hatása, amely alak-, illetve mozgásállapot-változásban nyilvánul meg. Ettől különböző meghatározás van az összefoglalásban: "erőhatás következtében a testek mozgásállapota, illetve alakja is megváltozhat.A különbség a feltételes mód! 
2/ Miért szoktuk HIBÁSAN azt mondani, hogy 1kg egyenlő 10 N-nal?

1/ A megengedő feltételes mód azt jelenti, hogy meg is történhet, de nem szükségszerű. Gondolj arra, amikor nagy erővel nyomsz egy nehéz szekrényt jópár másodpercig, mert odébb akarod tolni. Bele is izzadsz, akkora erőt fejtesz ki. Mégsem történik semmi. Tehát erőhatásra nem változik meg a szekrény mozgásállapota. Gondolj arra, hogy ráütsz egy asztalra. Nem változik az alakja, bár volt erőhatás. Bele is fájdult a kezed. Ellenben egy karate bajnok nagy erővel, keményen üt rá és ekkor eltörik. Alakváltozás. Nos ezért van a feltételes mód.

Miért írtam le ezt a látszólag jelentéktelen dolgot ilyen részletesen? Mert ez az apróság jól mutatja, hogy a fizikában pontosan, egzektul, korrekten kell foglamazni, különben rögtön ellenpéldát lehet mondani. Vagyis meg lehet cáfolni a pontatlan kijelentést.

A 2/ előtt pár erőfajtát mutatok be: i/ gravitációs erő, ii/ tartóerő, nyomóerő, iii/ súlyerő, iv/ súrlódási erő.

i) Gravitációs erő
Majdnem mindenki ismeri Newton almájának a történetét. Az alma leesett a fáról és így a mester nagy felismerésre jutott. Felfedezte, kimondta a gravitációt, a tömegvonzást. Tehát minden testre hat a Föld gravitációs ereje, minden testet vonz a Föld. Ezért esik függőlegesen lefelé minden elejtett test. Legyen az egy tollpihe vagy egy erkély az omladozó házról.
Sőt általában minden test, akármilyen kis tömegű is, vonzza a másik testet. 

 Az erő definíciójából kiolvasható és írják is a tankönyvek, hogy 1 N az az erő, amely 1kg tömeget 1 sec alatt álló helyzetből 1 m/sec sebességre gyorsít. Tehát az 1 kg-ot 1 sec² gyorsulással mozgat. Ehhez

Amint azt alaposan körbejártuk, tudható, hogy a test mozgásállapotát csak a környezete változtathatja meg. Kicsit részletesebben: a környezete által közvetített erőhatások ezen változások okai.

ISMÉTLÉS:
Mozgásállapot: a test helyzete és sebessége (iránya és nagysága) által meghatározott állapot.

A sebesség egy vektormennyiség, tehát nagysága mellett iránya is van. Természetesen a mértékegységéről se feledkezzetek el!!!

Ezek a fenti (környezeti) erők lehetnek mechanikai, elektromos, gravitációs vagy éppen mágneses erők is. A mechanikai egy közvetlen erőhatás, a többi itt felsorolt pedig fizikai erőtér által közvetített. (Emlékeztek? A Föld ~384 ezer km távolságból hat a Holdra és viszont.) Mechanikai erő pl. a gördülő vagy csúszó súrlódási, a húzó, az emelő, a tartó, a nyomó, vagy éppen a rugóerő. Bizonyára ti még többet tudtok mondani.

Ma azt vizsgáljuk meg, mi is az az erő? Indulj ki a saját fizikai erődből! Ha erővel ráütsz pl. egy tojásra, az összetörik. Ha erővel megrántasz, meglöksz egy játékautót, az gyorsulva elindul. Ilyen példákat sokáig lehet sorolni. Általánosságban azt lehet mondani és az erő, erőhatás szempontjából fontos, lényeges: Az erő, erőhatás következtében a testek mozgásállapota vagy alakja megváltozik/megváltozhat!

Vagy éppen nézzük a gépkocsi erejét a lóerőt (LE).

Ez a jelenleg legfürgébb TESLA Model S P100D, 840 LE-vel 2,28 másodperc alatt gyorsul 0-ról 100 km/h óra sebességre!

* A tapasztalatból tudható, hogy minél nagyobb az erőhatás,
- annál nagyobb a sebességváltozás ugyanannyi idő alatt vagy
- annál rövidebb idő alatt történik ugyanannyi sebességváltozás.
E mellett azt is tapasztaljuk, hogy minél nagyobb tömeg mozgásállapotát kell megváltoztatni, annál nagyobb erő szükséges hozzá. Gondoljatok a biciklitekre/rollerotokra és a gépkocsitokra.

E R Ő  (Definíció): Az a mennyiség, amely megadja az erőhatás nagyságát és irányát. Az erő jele az F.
A nagyság és az irány miatt az erő is vektormennyiség. A vektorokat nagyságukkal és irányukkal ábrázoljuk, tehát ez egy nyíl.

Azt a pontot, ahol az erőhatás a testet éri, az erő támadáspontjának nevezzük.

A támadásponton átmenő és az erőhatás irányába eső egyenest hatásvonalnak nevezzük. A támadáspontot az adott helyzethez igazodva az adott testen bárhová rajzolhatom a hatásvonalon.

Ennek az erővektornak kgm/sec² lesz a mértékegysége. Nézzük csak, miért is?

A fizika egyik legnagyobb alakja, angol tudós a XVII. században sokat foglalkozott az erővel. Kísérletei során ő is azt a megállapítást tette, amit az előbb felírtam és *-gal jelöltem:
Az erő által egy testen létrehozott gyorsulás (a) (=sebességváltozás) egyenesen arányos magával ezzel a gyorsítóerővel (F) és fordítottan arányos az adott test tömegével (m). Ez így kicsit bonyolultan hangzik, de ez a lényeg. Talán egyszerűbb, ha felírjuk

NEWTON II. TÖRVÉNYÉT: F = m * a

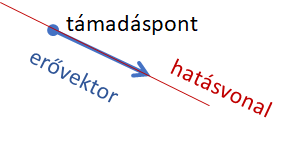
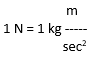Az erő egysége a newton - N. 1 newton az az erő (a II. törvény miatt), amely 1 kg tömegű nyugvó testet 1 másodperc alatt 1 m/sec sebességre gyorsít fel. Tehát a híres összefüggés: Alkalmazd rögtön a most megismert összafüggéseket egy mintapéldában:
Egy golyó tömege 1,5 kg. 2 másodperc alatt nyugalmi helyzetéből felgyorsítottam 5 m/sec sebességre. Mekkora erőt kellett ehhez kifejtenem?
m = 1,5 kg
v = 5 m/sec (0-ról)
t = 2 sec
-----------------

Érdekesség: 3,75 N egy 37,5 dkg-os tömeg súlya. Ugyanekkora erő kell ahhoz is, hogy az 5 m/sec pillanatnyi sebességű testet 10 m/sec sebességre gyorsítsam. Ugyanis mindkét esetben 5 m/sec a sebességváltozás!

Itt még egy érdekességre szeretném felhívni a figyelmeteket. De ezt már a következő posztban írom meg.

Az előző leckében írtam az alábbi két fogalomról:

1/ Először nézzük az átlagsebességet. Jele v_átl

A fenti átlag a test mozgását 'összefoglalóan' jellemzi. Ez torzíthat és lényeges információt takarhat el. Pl. 66 km-t tettünk meg 1 óra alatt 100 km/h 'állandó/egyenletes' sebességgel. Hogy lehet ez? Ugyanis a mozgás/haladás közbeni 100-as tempó mellett 20 percre megálltunk egy kávéra. Átlagsebességünk ettől romlott le 66 km/h-ra.
Lényeges jellemző, hogy ilyenkor VÁLTOZÓ MOZGÁST végeztünk. =>

Változó mozgást végző test átlagsebessége aTELJES út és annak megtételéhez szükséges TELJES idő hányadosa.
Világos, hogy egyenletes egyenes vonalú mozgás esetében bármely időtartamban az átlagsebességek egyenlők.

Vegyünk egy ELMÉLETI példát. Budakalászról a 90 km-re levő Dunaújvárosba autóúton 90 km/h állandó/egyenletes sebességgel 1 óra alatt érünk el, ahol átszállunk egy lassabb kocsiba és azonnal továbbindulunk. Pécsre (újabb 125 km) szintén állandó/egyenletes sebességgel, 62,5 km/h-val 2 óra alatt érkezünk meg. Mennyi a két szakaszra számított átlagsebesség? Semmiképpen sem a 90 és a 62,5 (számtani) átlaga! NEM 76,25 km/h!!!
Az átlagsebesség a teljes út hosszának és a teljes időtartmnak a hányadosa. v =s/t a teljes útra vonatkoztatva.
összes út = s = s[Bk-D] + s[D-P] vagyis 90km + 125km = 215km.
összes idő = t = t[Bk-D] + t[D-P] vagyis 1h + 2h = 3h
átlagsebesség =  v_átl = 215km / 3h = 71,6 km/h!!!           Tehát különbözik a számtani átlagként kapott értéktől.

2/ Másodszor pedig a változó mozgás miatt érdemes és szükséges még a pillanatnyi sebesség fogalmát is bevezetni. Ezt mutatja a Trafipax, a saját kilométeróránk a kocsiban vagy a Net sebességmérője.

   Jele v_pill

A pillanatnyi sebesség definíciója: Az a sebesség, amellyel a test egyenletesen mozogna tovább, ha ebben az adott pillanatban minden, a testet érő hatás megszűnne - az az erőhatás, amely ezt a sebességet létrehozta.

A pillanatnyi sebesség és az átlagsebesség SI mértékegysége a m/sec, illetve lehet pl. km/h. m/h, km/sec

!!! FONTOS megjegyezni, sokszor kell majd:  1 km/h = 1000 m/3600 sec = 1 m/3,6 sec  = > 1 m/sec = 3,6 km/h

Mindenképpen beszélnünk kell a sebességvektorról, a vektor fogalmáról.

A sebességnél tulajdonképpen két dolog számít. A nagysága, mértéke mellett iránya is van! Nem mindegy, merre mész pl. 60 km/h sebességgel. Budakalászról Északra indulva 1 óra múlva Szlovákiába érsz, Délre viszont Dunaújvárosba jutsz. Ezt a következőképpen ábrázoljuk, szemléltetjük.

A sebesség egy vektor. Ezt nem kell megérteni, megmagyarázni, ez definíció. A sebességnek iránya is és nagysága is van, tehát különbözik az olyan fizikai mennyiségektől, mint a hosszúság, tömeg, sűrűség. A matematikában az ilyen objektumot vektornak nevezik, tehát a sebesség is vektor. Rajzban egy nyílnak ábrázoljuk és az aláhúzott betűvel, ezúttal a v-vel jelöljük. Ha a sebesség nagysága kétszer nagyobb, akkor a nyíl hosszát kétszer nagyobbra (2v) vesszük. Háromnál (3v) ugyanígy. Ha pedig az irány különbözik akkor természetesen a nyilat a kívánt irányba rajzoljuk. v', v", v'".

FIGYELEM:
A tankönyv az aláhúzást nem használja, a sebességet az egyszerűség kedvéért símán a v betűvel jelöli.