Az előző órán ott hagytam abba, hogy az egyenletes mozgás lehet
- egyenes vonalú mozgás, pl. a mozgólépcső olyan lépcsőfoka, amelyik nem a fésűsfogak alatt fordul
- körmozgás, pl. a Hold közelítőleg körpályán kering a Föld körül időtlen-idők óta.
- bármilyen más alakú pályán mozgás.
(A körmozgás leírásával majd 2 lecke múlva folglakozunk)
Világos, hogy sokkal többször nem mozogsz egyenletesen, mert pl. futsz a HÉV után egyre gyorsabb tempóban, vagy a tesi órán a 400 méteres futás után a célban 'leeresztesz' és a gyors futás után pár lépés után megállsz. Hát még milyen egyenetlenül és cikk-cakkban fut a nyúl a róka elől.
Erről fogunk majd tanulni, amikor a gyorsuló mozgást vizsgáljuk. De persze egyszerűsítjük az életünket, csak az egyenes utat tanulmányozzuk.
Ha sétálsz egy sík mezőn levő egyenes földúton, akkor elég jó közelítéssel egyenes vonalú egyenletes a mozgásod. Milyen jellemzőket tudsz a saját mozgásodról mondani?
- a tested egy fizikai TEST, amit fizikai módszerrel vizsgálsz.
- a TESTeket a jellemző pontjukkal 'helyettesítjük', amint korábban megbeszéltük. Tehát elvonatkoztatsz a saját kiterjedésedtől, alakodtól. Mondjuk a köldöködet tekinted a jellemző pontnak.
==> a köldököd mozgása egyenes vonalú egyenletes mozgás!!! Ez volt az absztrakció.
Tehát mit tudsz mondani annak a pontnak a mozgásáról elmondani, ami most a köldököd? A pályáját le tudod írni pl. fél órán keresztül és az aktuális sebességét meg tudod adni ez alatt a fél óra alatt.
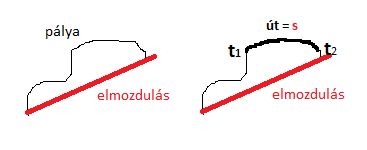
Általánosságban elmondható, hogy ismerjük a mozgást, a test mozgását, ha minden pillanatban meg tudjuk adni a helyzetét, hogy milyen úton mozog és ismerjük a sebességét.
Ezért tanuljuk ezeknél az egyszerű mozgásoknál az út-idő és a sebesség-idő összefüggéseket. Ez a mozgás legfontosabb, legkönnyebben tanulmányozható tulajdonsága.
Először az egyenletes mozgást nézzük meg. Azt mondjuk, hogy
egyenletes a mozgás, ha az egyenlő időközök alatt megtett utak hosszúságai egyenlők.
Nézzünk egy ilyen mozgást - emlékezzetek a Mikola csőre, amivel négyes csoportban mértetek az órán!
| időtartam |
1.től 5. se-cig = 4sec |
5.sec-9.sec-ig = 4sec |
9.sec-13.sec-ig = 4 sec |
13.-17.sec-ig = 4 sec
|
| megtett út |
142 mm |
144 mm |
139 mm |
142 mm |
A matematikában az ilyen összefüggést egyenes arányosságnak tanultátok. Ezt a fizikában is átvettük.
Egxenes arányosság tehát, ha a kétszer annnyi idő alatt kétszer annyi utat tesz meg a kocsi, négyszer annnyi idő alatt pedig négyszer annyi utat tesz meg.
Röviden azt mondhatjuk, hogy az út és az idő hányadosa állandó.
Ugyanis út/idő = 2*út / 2*idő = 4*út / 4*idő = 12*út / 12*idő.
Ezt a hányadost elnevezzük sebességnek. Ezt a köznapi beszédben tempónak is mondjuk. Tehát a definíció:
A sebesség az a fizikai mennyiség,
amely megmutatja, hogy a test egységnyi idő alatt milyen hosszú utat tesz meg.
Mert ugye, ha az idővel osztod, akkor azt kapod meg, hogy az időegységre mennyi út esik/jut. 50 km/h egy sebesség adat. Ez azt mutatja, hogy óránként hány kilométert haladsz. Itt az óra az időegység.
Térjünk vissza akkor az előző táblázatra!
| Időtartam |
1-5 sec = 4 sec |
4 sec |
4 sec |
4 sec |
ÁTLAG |
| megtett út |
142 mm |
144 mm |
139 mm |
143 mm |
142 mm |
| SEBESSÉG |
142mm/4sec = 35,5 mm/sec |
144mm/4sec = 36 mm/sec |
139mm/4sec = 34,75 mm/sec |
143mm/4sec = 35,75 mm/sec |
142mm/4sec = 35,5 mm/sec |
az időt a stopperrel igen pontosan, korrekten lehet mérni, ezért mindig 4 sec az eltelt idő.
Az átlagot már ismeritek, az órán ezt fújtátok: 4 mérés átlaga = a négy mérés összege osztva 4-gyel.
(9 mérés átlaga = a 9 mérés összege osztva 9-cel)
Azért mérünk többször, mert így a mérési hibákat ki tudjuk egyensúlyozni, és minél többet mérek, annál pontosabb az átlag. Végül pedig azt az átlagot fogadjuk el a mérés TÉNYLEGES eredményének.
Itt a négy mérés azt mutatta, hogy az egyenlő időközök alatt a buborék egyenlő utakat tett meg, az út/idő hányados ugyanaz => a sebesség ugyanaz => ez egy egyenes vonalú egyenletes (sebességű) mozgás!
Csak úgy próbaképpen nézzük meg az első két és az utolsó két szakasz sebességét:
- (142+144)mm / (4+4) sec = 286 mm / 8 sec = 35,75 mm/sec
- (139+143)mm / (4+4) sec = 282 mm / 8 sec = 35,25 mm/sec
a két hosszabb időtartamon számolva szinte ugyanannyi a sebesség. A kettő átlaga ugyanúgy 35,5 mm/sec, mint a négy kisebb és egyenlő szakasszal számított átlag.
Megint igazoltuk, hogy ez egy egyenes vonalú egyenletes (sebességű) mozgás!
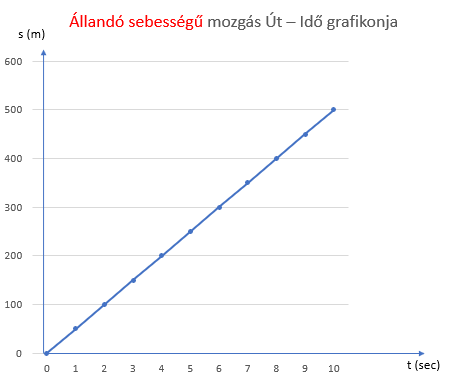
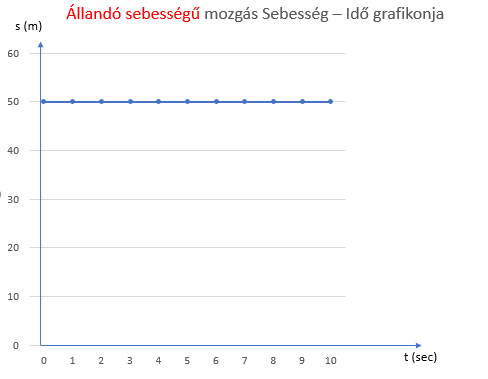
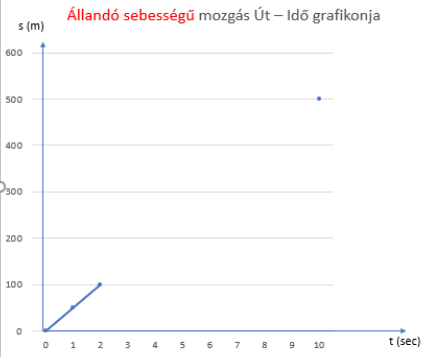
Nézzük meg ennek a mozgásnak a jellemző grafikonjait. Ábrázoljuk a megtett utat és az idő, majd a sebességet és időt együtt egy-egy grafikonon!
Tegyük egymás mellé a kettőt, tehát az út-idő grafikont és a sebesség-idő grafikont.
A bal oldali grafikon mutatja, hogy a mozgás valóban egyenletes, hiszen nyílegyenesen növekszik mind az idő, mind a hozzá tartozó (megtett) út értéke.
Az is látható, hogy kétszer annyi időhöz kétszer annyi, négyszer több időhőz négyszer hosszabb út tartozik. Bármelyik pont két koordinátáját veszed és elosztod azokat, ugyanakkora a hányados. Ez a sebesség, pl. 400/8 = 200/4 = 50 m/sec. Ez ugye az egyenes arányosság.
Vegyétek észre, hogy ha meredekebb az egyenes, akkor nagyobb lesz az előbbi hányados, tehát a sebesség.
A jobb oldali grafikonról pedig egyszerűen le lehet olvasni, hogy mennyi a sebesség. Amilyen magasan van a vizszintes egyenes. Világos, ha állandó a sebesség, akkor minden időpillanatban ugyanakkora értéket kell berajzolnunk.
Még két fogalom a végére:
A pillanatnyi sebesség, amit pl. a gépkocsi kilométerórája jelez: az a sebesség, amivel Newton I. miatt a test tovább mozogna, ha további kölcsönhatás nem érné (hirtelen üresbe tennét a kocsit)
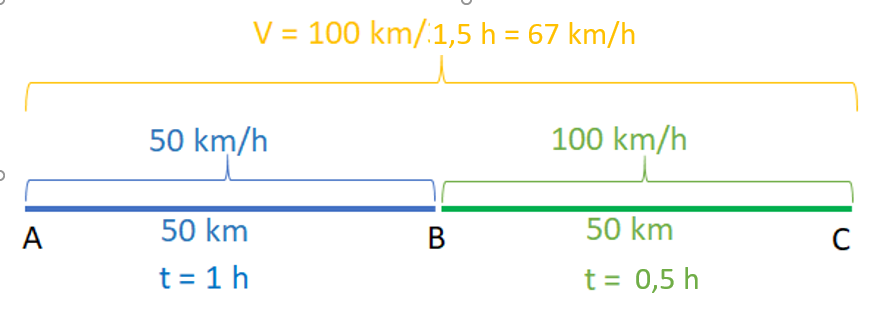
Átlagsebesség: a teljes útszakasz hossza osztva az összes eltelt idővel.
Tehát ha 100 km-t 10 km/h sebességel hajtottál, majd újabb 100 km-t 100 km/h-val, akkor az átlagsebesség a 200 km-re számolva nem 55 km/h!!! Miért? az első 100 km-t 10 óra alatt, a második 100 km-t 1 óra alatt tetted meg. a teljes időtartam tehát 11 óra, a teljes út 200 km. Így az átlagsebesség 200 km / 11 óra = 18,2 km/h. Meglepődtél?
Hf: Munkafüzet 14. oldal 1-4 feladatok
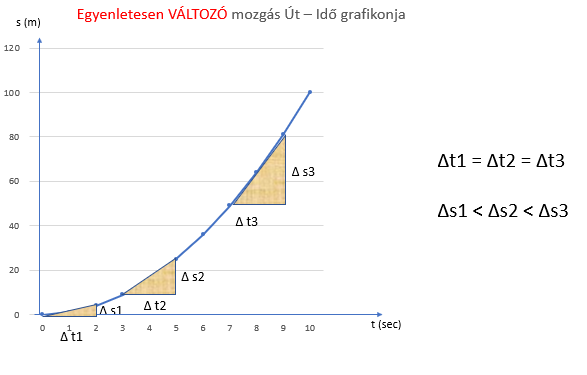 A már megismert ÚT-IDŐ grafikont rajzoltam ide. Az azonos időegység alatt megtett utak egyre nagyobbak. Ezt fejezi ki a görbe mellett a három darab háromszög egyre magasabb csúcsa. Amint odaírtam, az időkülönbségek, tehát a Δt-k egyenlők és a Δs-ek egyre nagyobbak, ahogy múlik az idő. Az egyenlőtlenségből következik, hogy a Δs/Δt hányadosok egyre nagyobbak.
A már megismert ÚT-IDŐ grafikont rajzoltam ide. Az azonos időegység alatt megtett utak egyre nagyobbak. Ezt fejezi ki a görbe mellett a három darab háromszög egyre magasabb csúcsa. Amint odaírtam, az időkülönbségek, tehát a Δt-k egyenlők és a Δs-ek egyre nagyobbak, ahogy múlik az idő. Az egyenlőtlenségből következik, hogy a Δs/Δt hányadosok egyre nagyobbak.  .
.

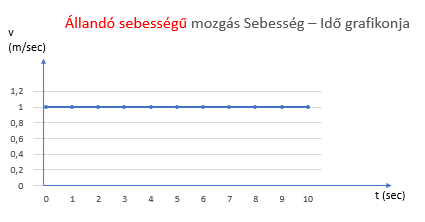 Jól jegyezzétek meg, a sebesség állandó, tehát a grafikonja ez a vizszintes egyenes. Persze, mert a sebesség értéke állandó, tehát minden időpillanatban, minden időérték felett ugyanolyan magasan kell a pontot rajzolni.
Jól jegyezzétek meg, a sebesség állandó, tehát a grafikonja ez a vizszintes egyenes. Persze, mert a sebesség értéke állandó, tehát minden időpillanatban, minden időérték felett ugyanolyan magasan kell a pontot rajzolni.