Remélem, észrevettétek, hogy az előző lecke a nyomás fogalomról, fizikai mennyiségről szólt, de csak a szilárd testekről, a szilárd testek által kifejtett nyomásról. Most viszont továbbmegyünk, a nyugvó folyadékokban fellépő nyomással fogunk ismerkedni. Ezt hívjuk hidrosztatikai nyomásnak.
Először fejtsük meg, mit is jelent ez az új szó? Szóösszetételekben a 'hidro' vizet, vizest jelent, a 'sztatika' jelentése pedig nyugvó, egyensúlyban levő. Tehát ez a lecke a nyugalomban levő víz, illetve általánosabban a nyugvó folyadékok nyomásáról szól, mert a víz csak egy konkrét példa és minden folyadék hozzá hasonlóan viselkedik a nyomás szempontjából.
Nézzük meg, a folyadékokban is a súlytól származik a nyomás? Igaz, hogy a folyadékok hidrosztatikai nyomása a folyadék súlyából származik? Persze, hogy igen. Ezt azzal tudjuk bizonyítani, hogy egy gumihártya kidudorodását figyeljük és elfogadjuk, megállapodunk abban, hogy a hártya kidudorodásának mértéke a nyomás mértékét jelzi! Mi mást jelezne? Töltsünk vizet a luftballonba, helyezzünk rá egy nehezéket, fújjuk fel. Ugye ez mind a nyomást növeli és a hártya megnyúlásával jár. Tehát megegyezhetünk, hogy a nyomás és szűkebben a folyadék nyomása arányos a hártya megnyúlásával. Pontosabban is fogunk majd mérni, az a manométer* (=nyomásmérő) lesz.
A hidrosztatikai nyomás kiszámítását a poszt végén mesélem el.
A másik megfigyelés, ami ide tartozik, hogy amint lejjebb és lejjebb úszol a tóban, tengerben, egyre jobban feszít a füled, ami azt jelenti, hogy a füledben NŐ a NYOMÁS.
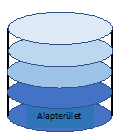 A folyadékoknak is van súlya, tehát ez is nyomást gyakorol az alátámasztási felületre. De mi a folyadék esetében ez a fix felület, amikor itt a molekulák szabadon mozognak egymáshoz képest? Nos itt is tetten érhetjük a fizika modellalkotását. Tegyük fel, hogy a folyadékot rétegekre osztjuk, amint ez a kis ábra mutatja és akkor már a szilárd testeknél tárgyalt és elfogadott nyomás fogalma alkalmazható.. Ez leegyszerűsítés, de tükrözi a valóságot és segít egy fizikai mennyiség megmagyarázásában, megértésében. Ezt jelenti a modellezés. Pontosan úgy, mint amikor kis autómodellel játszol. Olyan mint az igazi, a számodra érdekes lényeget, az alakot és a mozgékonyságot mutatja, tükrözi.
A folyadékoknak is van súlya, tehát ez is nyomást gyakorol az alátámasztási felületre. De mi a folyadék esetében ez a fix felület, amikor itt a molekulák szabadon mozognak egymáshoz képest? Nos itt is tetten érhetjük a fizika modellalkotását. Tegyük fel, hogy a folyadékot rétegekre osztjuk, amint ez a kis ábra mutatja és akkor már a szilárd testeknél tárgyalt és elfogadott nyomás fogalma alkalmazható.. Ez leegyszerűsítés, de tükrözi a valóságot és segít egy fizikai mennyiség megmagyarázásában, megértésében. Ezt jelenti a modellezés. Pontosan úgy, mint amikor kis autómodellel játszol. Olyan mint az igazi, a számodra érdekes lényeget, az alakot és a mozgékonyságot mutatja, tükrözi.
A legfelső réteget nem nyomja folyadék, tehát itt 0 a folyadék súlyából származó nyomás. (most a modellezés miatt eltekintünk a levegő nyomásától, ami, remélem eszdbe jutott). Alatta viszont már egy réteget kell hordozni, tehát ez már egy egységnyi nyomás. A felülről harmadik (picit sötétebb) réteget már két réteg nyomja, ami miatt itt már két egységnyi a nyomás. .... A legalsó (legsötétebb) réteget már az összes felette levő réteg nyomja, tehát itt a legnagyobb (ábránkban 4 egység) a nyomás.
Ebből következik, hogy a folyadékokban a folyadékoszlop magasságával - h - arányos a nyomás.
p ~ h.
|
|
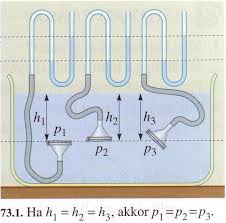
Ezt az itt bemutatott kísérlet is igazolja, amikor a csőre húzott gumihártya a magasabb vízoszlopnál nyúlt meg legjobban. |
|
|
Ugyanezt mutatja ez a másik elrendezés. A kilyukasztott kémcső legalsó nyílásán lövelli legmesszebb a vizet, ami az előbbiek értelmében szintén azt jelenti, hogy a nagyobb vízoszlop hidrosztatikai nyomása nagyobb. |
|
|
Hasonlóképpen lehet belátni, hogy minél 'nehezebb', sűrűbb a folyadék, nyomása is annál nagyobb. Emlékezz arra, mi történt az órán, amikor a vízbe sót öntöttem, vagyis növeltem a sűrűségét. Ismét jobban megnyúlt gumihártya. A harmadik képen a sötétebb folyadék egy fém oldott állapotban. Ugyanakkora magasságú folyadékoszlop esetében a gumihártya megnyúlása annál nagyobb, tehát a nyomás annál nagyobb, minél sűrűbb a folyadék. A folyadékokban a folyadék sűrűségével - ρ - arányos a nyomás. p ~ ρ. Ez a "ró" betű. ISMÉTLÉS: a sűrűséget a második, harmadik fizika órán tanultuk, lapozz oda! |
|
|
Azt is tudtam igazolni a hártya mozgatásával, hogy az adott folyadék hidrosztatikai nyomása ugyanolyan mélységben minden irányban egyenlő nagyságú, vagyis a hidrosztatikai nyomás nem irányfüggő.
|
A fentiek szerint a folyadékok nyomása, vagyis a hidrosztatikai nyomás két tényezőtől függ és mindkettővel egyenesen arányos. Függ:
- a folyadékoszlop magasságától,
- a folyadék sűrűségétől.
Mértékegysége ugyancsak Pa, mint a szilárd testeknél. Még szép, furán nézne ki, ha a kétfajta nyomásnak más lenne a mértékegysége. Természetesen 1000 Pa = 1 kPa (kilopascal) és ez a nyomás SI mértékegysége.
Tán hallottátok még a másik mértékegységet is említeni, ez a bar**, illetve a kilobar. Ez nem a szabványos SI m.e.
|
|
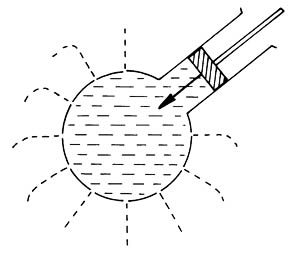
Még egy kísérletet végezz el gondolatban. Ez is le van írva a tankönyv 47. oldalán. (Érdemes még ezen az oldalon az előző kísérletet is elolvasni, elképzelni.) Nyomd meg a képen látható vizibuzogány dugattyúját! Minden irányban szinte azonos nyomással fröcsköl ki a víz. Ez a megállapítás már Pascal törvénye. Nyugvó folyadékban a külső nyomás a folyadék belsejében mindenhol ugyanannyival növeli meg az ott levő hidrosztatikai nyomást. |
Ezen a Pascal törvényen alapszik a hidrosztatika egy észszerű alkalmazása, a hidraulikus emelő működése:
Az A1 felületen megnyomom a dugattyút. Ennek hatására a négyszer nagyobb A2 felületen ugyanannyival emelkedik a nyomás (=F/A).
Tehát az F1/A1 = F2/A2 egyenletből látható, hogy A2>A1 miatt ez (Pascal) törvényszerűen az F2>F1 relációt jelenti. Ugyanis ebben a konkrét esetben az F1/A1=F2/A2 egyenlőség akkor marad érvényben az A2 helyére 4*A1-et írva, ha F2 helyére 4*F1-et írok. F1/A1=4*F1/4*A1. Ami bennünket érdekel: F2 erő, vagyis a teher négyszerese az F1 erőnek.
Tehát nagyobb súlyt/terhet lehet imígyen megemelni! Itt meg kell említeni, hogy csak erőt nyerünk, de munkát, energiát NEM! Gondolkozz el, miért?
Még egy fontos összefüggésre hadd térjek ki! Azt állapítottuk meg, hogy a folyadékok nyomása, vagyis a hidrosztatikai nyomás két tényezőtől függ és mindkettővel egyenesen arányos. Függ:
- a folyadékoszlop magasságától,
- a folyadék sűrűségétől.
Mást nem említettem, tehát CSAK e kettő befolyásolja a NYUGVÓ FOLYADÉK hidrosztatikai nyomását.
FIGYELEM, ezek után logikus a következtetés, hogy például a folyadék színétől, hőmérsékletétől nem függ. Tehát
NEM FÜGG a folyadékot tartalmazó edény alakjától (állhat ferdén is!) és főleg nem függ az edény szélsségétől, az aljának kiterjedésétől, bármekkora legyen is az!
|
* a -méter a szóösszetételek részeként a fizikában mindig -mérőt, -mérést jelent. barométer, kronométer, voltméter, amperméter, termométer, ... Példaként itt a skálával ellátott manométer: ** Jó tudni: 1 méter mélyen a víz hidrosztatikai nyomása 10.000 Pa. De vigyázz, ez a víz súlyából származó nyomás! Mivel a víz felszínét a levegő súlya is nomja, nyilván a víz felszínén (h = 0) nem 0 a nyomás, hanem már a normál légköri nyomás érvénysül. 1 m mélyen valójában 10.000 Pa + a légköri nyomást mutatja a manométer. |
 |
Hf: Munkafüzet 39. oldal 1, 2, 4, 5, és 40. oldal 7, 11 feladatokat megoldani.
Nézzük, hogy számoljuk ki a hidrosztatikai nyomást!
A már megtanult képlet: p = F/A érvényes a folyadékokban is, bár más alakban. Ez kicsit nehéz, de a végeredmény ígéretes. Tehát varázsoljunk:
 |
p = F/A = súlyerő/alapterület = (m*g)/A = (ρ*V*g)/A = (ρ*A*h*g)/A = nehézségi gyorsulás: 9,81 m/sec2 A m/sec2 felírható N/kg alakban is: (m*kg/sec2)/kg = N/kg, EZT IGAZOLHATJUK MÉRÉSSEL, KÍSÉRLETTEL IS. Nézzük az új képlet mértékegységét: ρ*h*g = kg/m3*m*N/kg =N/m2 Ezt akartuk bizonyítani. Ezt nem kell tudni, csak a két jelenség összefüggése miatt mutattam be ezt nektek!!! |